dLLM-RL
Reinforcement Learning for Diffusion Language Models
Reinforcement learning is an important methodology to improve language models. We propose the RL framework for discrete diffusion language models (see paper), paired with the most comprehensive post-training repository for dLLMs, and released models.
Insights Overview
- Prior methods omit trajectory awareness, leading to a mismatch between optimization and inference. In practice, diffusion language models employ confidence-driven sampling, which differs from the purely random sampling used in image diffusion.
- Building on this, we propose TraceRL, a trajectory-aware RL method applicable to both full- and block-attention DLMs. With trajectory shrinkage and sliced block training, we accelerate training.
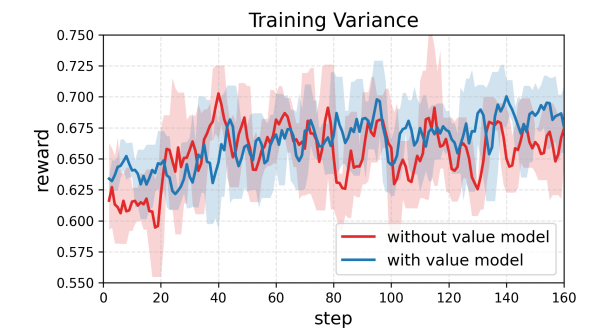
- We introduce a diffusion value model to stabilize training via token-wise variance-reduction baselines.
- We open-source a comprehensive post-training repo dLLM-RL for current open-source diffusion language models, including multiple SFT and RL methods, across math, coding, multimodal and RLHF settings, support process reward model and single/multiple nodes training.
- We also implement a 8B long-CoT block diffusion model. Based on our findings, traditional full-attention DLMs cannot handle long-context settings well; block diffusion is likely to become the dominant approach.
Trajectory matters for DLM post-training
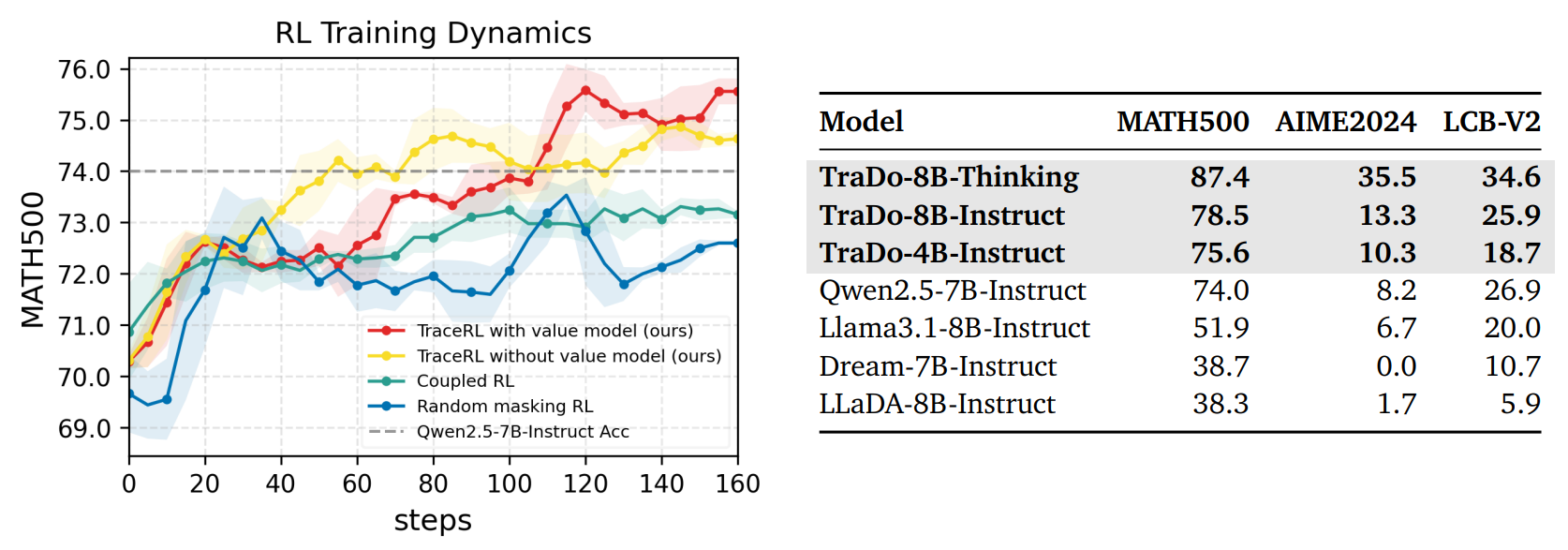
This is a simple demonstration experiment comparing different SFT methods for DLMs. Fully random masking is the commonly used SFT approach for full-attention DLMs. However, it overlooks the inherent logical structure of language, especially in reasoning tasks. Semi-AR SFT is the typical training method for block diffusion models: it applies random masks within each block while preserving block-wise causality. But applying Semi-AR training to full-attention models is slow because it requires slicing the data. We also explore trace-wise SFT, where a DLM collects its own confidence-driven trajectories and uses them for self-SFT. We find that, under comparable training time, fully random < Semi-AR < trace-wise.
TraceRL
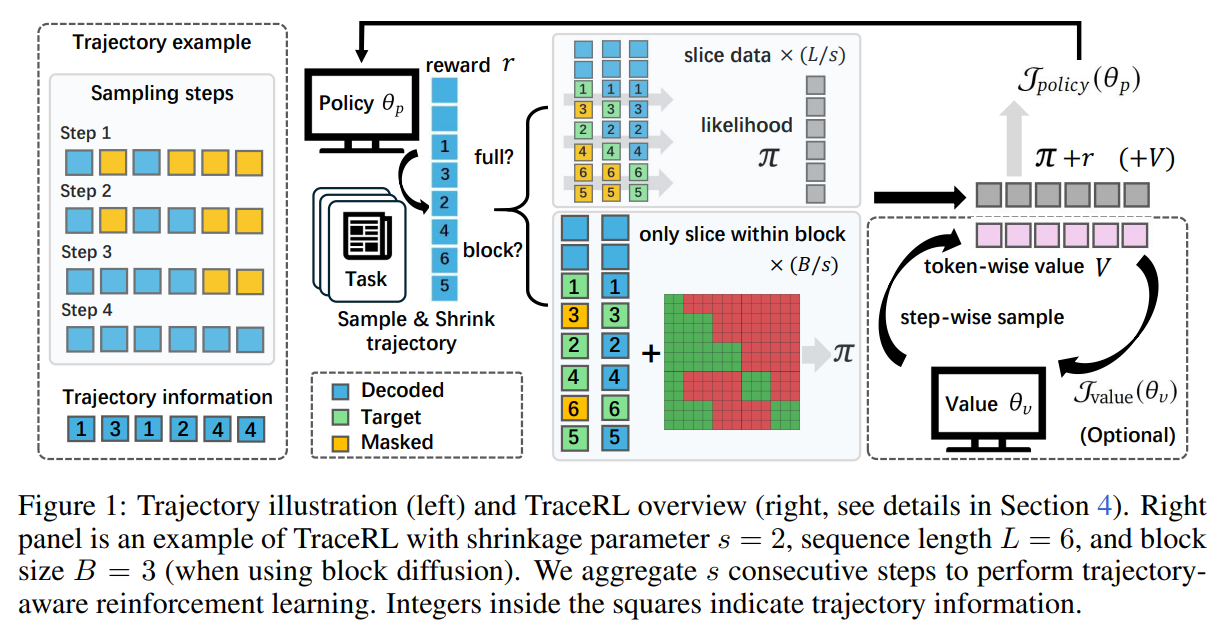
Given the above insights, we propose TraceRL. For each generated response \(\tau_i\) given the task \(Q\), we represent it as a trajectory
\[\tau_i \triangleq \tau_i(1) \cup \cdots \cup \tau_i(|\tau_i|),\]where \(|\tau_i|\) is the number of decoding steps, and \(\tau_i(t)\) is the set of tokens decoded during the \(t\)-th step. TraceRL rewards or penalizes the sampling trajectory under policy \(\pi_\theta\) based on the verifiable reward \(r_i\) assigned to \(\tau_i\). When using RLVR, \(r_i\) is equivalent to the verifiable outcome.
To accelerate training, we aggregate every \(s\) neighboring steps. Specifically, we compress \(\tau_i\) into
\[\tau_i^{s} \triangleq \tau_i^{s}(1) \cup \cdots \cup \tau_i^{s} (|\tau_i^{s}|),\]where
\[\tau_i^{s}(k) \triangleq \bigcup_{j=s(k-1)+1}^{\min(sk,\,|\tau_i|)} \tau_i(j), \qquad |\tau_i^{s}| = \left\lceil \frac{|\tau_i|}{s} \right\rceil.\]The policy loss is
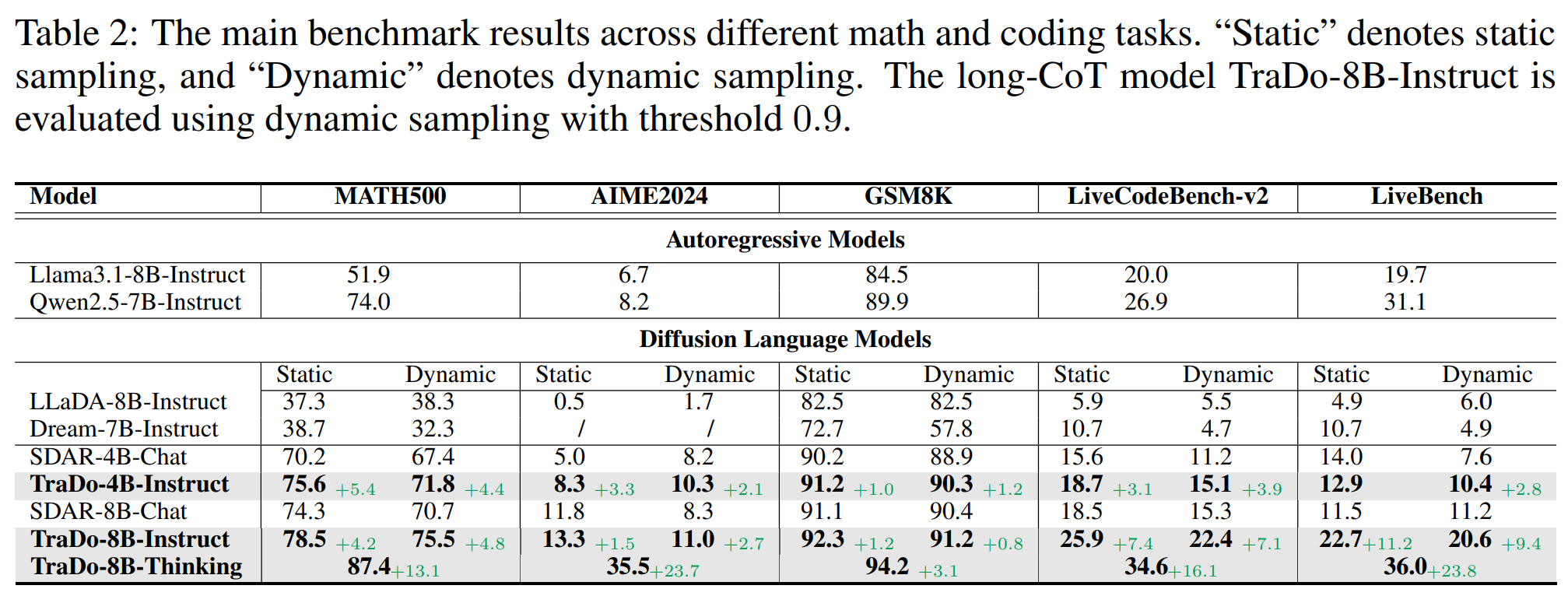
\[J_{ policy}(\theta_p) = E_{ \{ \tau_i \}_{i = 1}^G \sim \pi_{old}(\cdot \mid Q) } \Bigg( \sum_{i=1}^{G} \sum_{t=1}^{|\tau_i^{s}|} \frac{1}{|\tau_i^{s}(t)|} \sum_{o_k \in \tau_i^{s}(t)} C_{\epsilon}\!\left( \frac{\pi_{\theta_p}\!\left(o_k \mid \tau_i^{s} (1{:}(t-1))\right)} {\pi_{old}\!\left(o_k \mid \tau_i^{s}(1{:}(t-1))\right)}, A_i \right) \Bigg) - \beta\,\mathrm{KL},\]where the advantages are standardized based on the rewards. TraDo Instruction models are trained solely with RL based on SDAR models, see results below.
Diffusion Value Model
Diffusion value model provides a token-wise variance-reduction baseline. In our approach, we firstly derive step-wise rewards \(r_t^{\star}\) from token-wise rewards \(r_j\), and derive step-wise baseline values \(V_t^{\star, old}\) from the value model’s token-wise outputs \(V_j^{old}\). Specifically,
\[r_t^{\star} = \frac{1}{|\tau(t)|} \sum_{j \in \tau(t)} r_j, \,\,V_t^{\star, old} = \frac{1}{|\tau(t)|} \sum_{j \in \tau(t)} V_j^{old},\]where the \(V_j^{old}\) are derived from value model following the same inference trajectory of \(\tau\). Then we can derive the step-wise returns \(R_t^{\star}\) and GAE \(\delta_{t}^{\star}\):
\[R_t^{\star} = r_t^{\star} + \gamma R_{t + 1}^{\star}, \,\, R_{|\tau| + 1}^{\star} = 0, \,\, \delta_{t}^{\star} = r_t^{\star} - V_t^{\star, old} + \gamma V_{t + 1}^{\star, old}.\]The step-wise advantages \(A_t^{\star}\) is defined as:
\[A_t^{\star} = \sum_{k = 0}^{|\tau| - t} (\gamma \lambda)^k \delta_{t+k}^{\star}, \,\, A_{|\tau| + 1}^{\star} = 0, \,\, V_{|\tau| + 1}^{\star, old} = 0.\]Finally, we obtain the token-wise quantities:
\[R_j = r_j + \gamma R_{t_j + 1}^{\star}, \,\, A_j = r_j - V_{j}^{old} + \gamma V_{t_j + 1}^{\star, old} + \gamma \lambda A_{t_j + 1}^{star}.\]The token-wise advantages \(A_j\) are used in policy model’s objective function. Value model’s objective function is designed to align value model’s output with the token-wise returns \(R_j\):
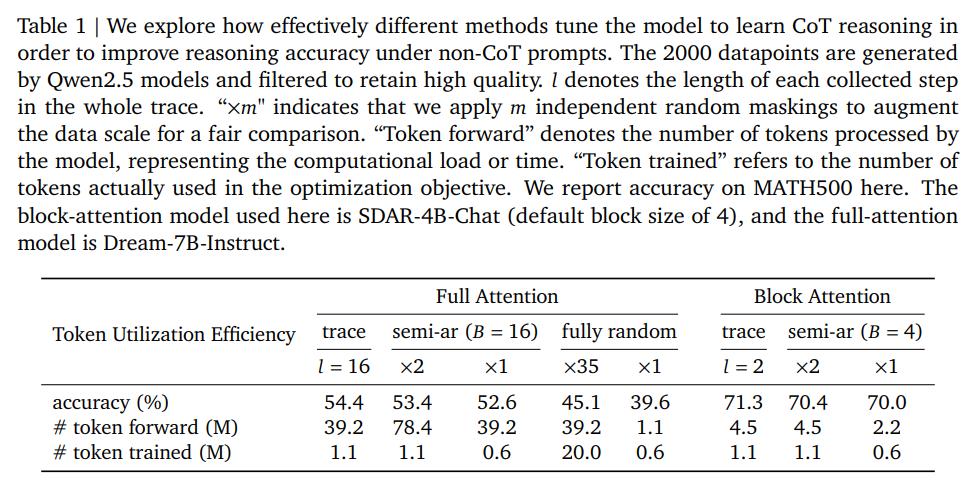
\[J_{value}(\theta_v) = \frac{1}{2} E_{\tau} \left[ \frac{1}{|\tau|} \sum_{j \in \tau} max ((V_{\theta_v}(\tau)_j - R_j)^2, (V_j^{clip} - R_j)^2) \right].\]See the following table, using value model can drop 45.5% variance in training.
Long-CoT Models & Importance of Block Diffusion
We select 75K long-CoT samples from Openthoghts3-1.2M to conduct SFT to TraDo-8B-Instruct model, resulting in TraDp-8B-Thinking model. Note that full-attention models cannot handle long-context settings well, because the prefill pass is extremely computationally expensive for long contexts. We believe the future of diffusion language models lies in block diffusion.
@article{wang2025revolutionizing,
title={Revolutionizing reinforcement learning framework for diffusion large language models},
author={Wang, Yinjie and Yang, Ling and Li, Bowen and Tian, Ye and Shen, Ke and Wang, Mengdi},
journal={arXiv preprint arXiv:2509.06949},
year={2025}
}
Some related works on dLLM: SDAR, LLaDA, Dream, block diffusion, Fast-dLLM.